Zdravstvena škola Split

Fibonaccijev niz

KNJIŽICA FORMULA - viša razina

http://dokumenti.ncvvo.hr/Ispitni_katalozi_12-13/Dodatci/formule_mata.pdf

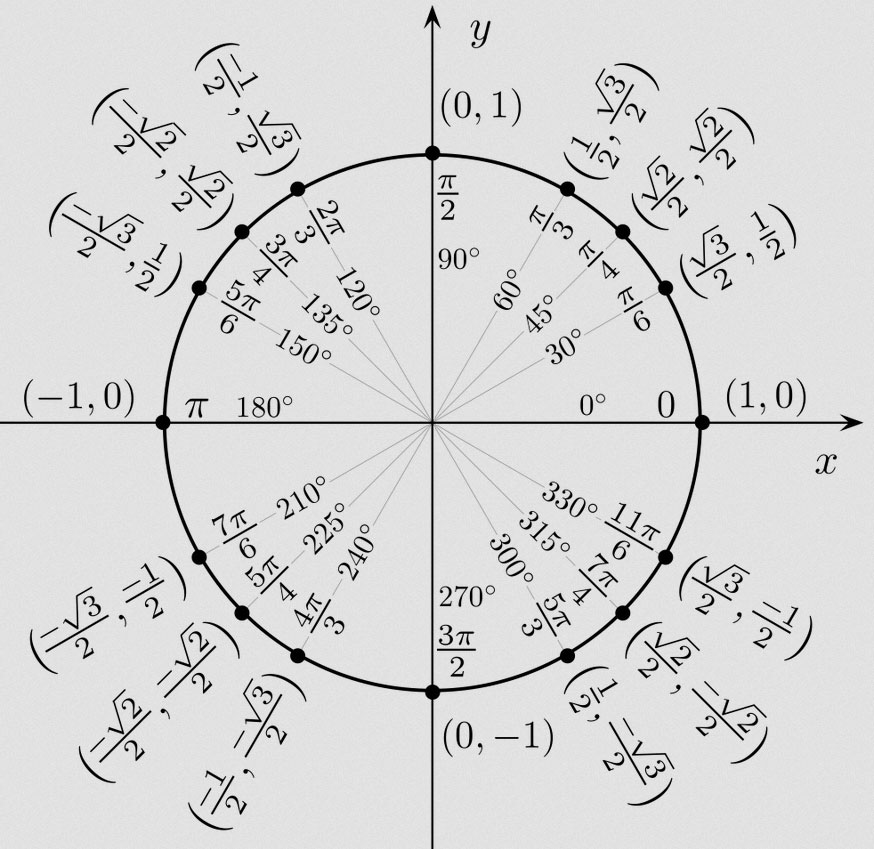
Brojevna kružnica

Namatanje brojevnog pravca na kružnicu (bez rastezanja i klizanja). Svakom broju pridružuje se jedna točka kružnice. Naglašene su samo istaknute točke kružnice.

Kliknite na gumb za pokretanje animacije u donjem lijevom kutu apleta ili povlačite klizač t.

Dragi moji, ovdje se nalazi riješen zadatak iz Brojevne kružnice.

Zadatak 4. b)

Definicije trigonometrijskih funkcija

Vrijednosti trigonometrijskih funkcija nekih karakterističnih brojeva (kutova)

Dragi moji, 

• pogledajte ovaj VIDEO.

Do sada je naš Homer živio u svijetu sa samo dvije dimenzije - svijetu u kojem je poznavao samo visinu i širinu.  Uz ovaj nadasve poseban svijet, Homer prelazi i u jedan još uzbudljiviji svijet, svijet u kojem će otkriti i treću dimenziju. O tom novom 3D svijetu Homera svoja zapažanja ćete zapisati pomoću ovog alata. 

Nemoguće figure (iluzije) trijumf su mašte i razigranosti nad realnošću. 

1. ZADATAK 

Konstruiraj nemoguće figure prikazane na sljedećim slikama u izometrijskoj trokutastoj mreži točaka. 

• Konstruiraj projekciju geometrijske figure složene od kockica u kvadratnoj mreži.
• Konstruiraj projekciju bilo koje geometrijske figure.
• Konstruiraj geometrijske figure prema zadanim projekcijama u izometrijskoj trokutastoj mreži točaka, pri čemu je preporuka već zadane projekcije prvo nacrtati/konstruirati u kvadratnoj mreži i time odrediti dimenziju.

IZOMETRIJSKA TROKUTASTA MREŽA TOČAKA

2. ZADATAK

• Izradi trodimenzionalni model od kartona, dio kojeg, gledate li iz točno odredenog kuta, vidite kao nemogući trokut (1. Geometrijska figura). 

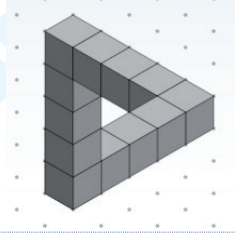
          1. Geometrijska figura                           2. Geometrijska figura

___________________________________________________________________________________________________________________________

UPITNIK ZA UČENIKE 

___________________________________________________________________________________________________________________________

DOMAĆI RAD:

• konstruiraj nemoguće stepenice u nevidljivoj izometrijskoj trokutastoj mreži
• pogledajte dokumentarac o M. C. Escheru i napišite kratak osvrt
• ponovno pogledajte video Treehouse of Horror i dublje istražite tu pozadinsku matematiku

ZA ONE KOJI ŽELE VIŠE

 Ponovo i detaljno pogledajte video Homer3 te istražite:

• Što je Utah teapot?
• Kakva je veza između jednakosti 178212 + 184112 = 192212 i Fermata?
• Što je Eulerov identitet?
• Je li P = NP?
• Što su Milenijski problemi?
• Što znači 46 72 69 6E 6B 20 72 75 6C 65 73 21 (heksadekadski ASCII kod)?

Koliko ja znam, u postojanju objektivne stvarnosti nema nikakvog dokaza do li naših osjetila,a ne vidim zašto bismo vanjski svijet prihvatili kao takav jedino zbog naših osjetila. U svojim grafičkim oblicima nastojim pokazati da živimo u lijepom i urednom svijetu a ne, kao što nam se to neki put priča, u kaosu bez normi. Ne mogu si pomoći a da se ne izrugujem svim našim nepokolebivim sigurnostima. Primjerice vrlo je zabavno pobrkati dvije i tri dimenzije, ravninu i prostor, ili šaliti se s gravitacijom. 
Jeste li sigurni da pod ne može biti strop? Jeste li apsolutno sigurni kad se uspinjete uz stepenice da se penjete prema gore? Dobro ne može postojati bez zla, i ako se prihvati Bog, mora se s druge strane istovrijedno mjesto dati i đavlu. To je ravnoteža. Ja živim od te dualnosti.

                                                                                                          Esher